Circuitos serie RL y RC
Figura 6: Circuitos serie RL (superior) y RC (inferior) en
CC.
Figura 7: Comportamiento de los circuitos serie RL y RC en CC.
Los circuitos serie RL y RC (figura 6) tienen un comportamiento similar en cuanto a su respuesta en corriente y en tensión, respectivamente.
Al cerrar el interruptor S en el circuito serie RL, la bobina crea una fuerza electromotriz (f.e.m.) que se opone a la corriente que circula por el circuito, denominada por ello fuerza contraelectromotriz. Como consecuencia de ello, en el mismo instante de cerrar el interruptor (t0 en la figura 7) la intensidad será nula e irá aumentando exponencialmente hasta alcanzar su valor máximo, Io = E / R (de t0 a t1). Si a continuación, en el mismo instante de abrir S (t2 en la figura 7) se cortocircuitara la red RL, el valor de Io no desaparecería instantáneamente, sino que iría disminuyendo de forma exponencial hasta hacerse cero (de t2 a t3).
Por otro lado, en el circuito serie RC, al cerrar el interruptor S (t0 en la figura 7), el condensador comienza a cargarse, aumentando su tensión exponencialmente hasta alcanzar su valor máximo E0 (de t0 a t1), que coincide con el valor de la f.e.m. E de la fuente. Si a continuación, en el mismo instante de abrir S (t2 en la figura 7) se cortocircuitara la red RC, el valor de Eo no desaparecería instantáneamente, sino que iría disminuyendo de forma exponencial hasta hacerse cero (de t2 a t3).
En ambos circuitos se da por lo tanto dos tipos de régimen de funcionamiento (figura 7):
- Transitorio: desde t0 a t1 (carga) y desde t2 a t3 (descarga)
- Permanente: desde t1 a t2
La duración del régimen transitorio depende, en cada circuito, de los valores de la resistencia, R, la capacidad, C, del condensador y de la autoinductancia, L de la bobina. El valor de esta duración se suele tomar como 5τ, donde τ es la denominada constante de tiempo, siendo su valor en cada circuito:
Si R está en ohmios, C en faradios y L en henrios, τ estará en segundos.
Matemáticamente se pueden obtener las ecuaciones en régimen transitorio de cada circuito que se muestran en la siguiente tabla:
| Carga en RL |
Descarga en RL |
Carga en RC |
Descarga en RC |

 |

 |

 |

 |
Circuitos de corriente alterna
En el presente apartado se verán las caraterísticas de los circuitos básicos de CA senoidal que están formados por los componentes eléctricos fundamentales: resistencia, bobina y condensador (ver previamente su comportamiento en DC). En cuanto a su análisis, todo lo visto en los circuitos de corriente continua es válido para los de alterna con la salvedad que habrá que operar con números complejos en lugar de con reales. Además se deberán tener en cuenta las siguientes condiciones:
- Todas las fuentes deben ser sinusoidales y tener la misma frecuencia o pulsación.
- Debe estar en régimen estacionario, es decir, una vez que los fenómenos transitorios que se producen a la conexión del circuito se hayan atenuado completamente.
- Todos los componentes del circuito deben ser lineales, o trabajar en un régimen tal que puedan considerarse como lineales. Los circuitos con diodos están excluidos y los resultados con inductores con núcleo ferromagnético serán solo aproximaciones.
Circuito serie RL
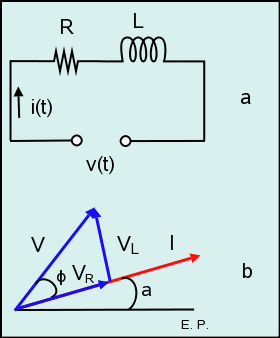
Figura 8: circuito serie RL (a) y diagrama fasorial (b).
Supongamos que por el circuito de la figura 8a circula una corriente

Como VR está en fase y VL adelantada 90º respecto a dicha corriente, se tendrá:
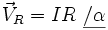

Sumando fasorialmente ambas tensiones obtendremos la total V:
donde, y de acuerdo con el diagrama fasorial de la figura 8b, V es el módulo de la tensión total:
y φ el águlo que forman los fasores tensión total y corriente (ángulo de desfase):

Figura 9: triángulo de impedancias de un circuito serie RL.
La expresión  representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina impedancia y se representa Z:
representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina impedancia y se representa Z:

En forma polar

con lo que la impedancia puede considerarse como una magnitud compleja, cuyo valor, de acuerdo con el triángulo de la figura 9, es:

Obsérvese que la parte real resulta ser la componente resistiva y la parte imaginaria la inductiva.
Circuito serie RC
 Figura 10
Figura 10: Circuito serie RC (a) y diagrama fasorial (b).
Supongamos que por el circuito de la figura 10a circula una corriente

Como VR está en fase y VC retrasada 90º respecto a dicha corriente, se tendrá:
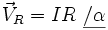

Figura 11: Triángulo de impedancias de un circuito serie RC.
La tensión total V será igual a la suma fasorial de ambas tensiones,
Y de acuerdo con su diagrama fasorial (figura 10b) se tiene:

Al igual que en el apartado anterior la expresión  es el módulo de la impedancia, ya que
es el módulo de la impedancia, ya que

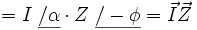 lo que significa que la impedancia es una magnitud compleja cuyo valor, según el triángulo de la figura 11, es:
lo que significa que la impedancia es una magnitud compleja cuyo valor, según el triángulo de la figura 11, es:
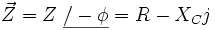
Obsérvese que la parte real resulta ser la componente resistiva y la parte imaginaria, ahora con signo negativo, la capacitiva.
Circuito serie RLC
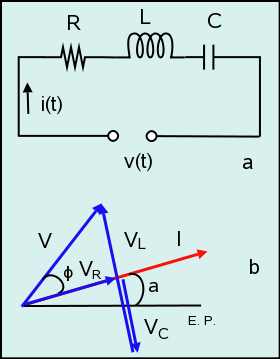
Figura 12: Circuito serie RLC (a) y diagrama fasorial (b).
Razonado de modo similar en el circuito serie RLC de la figura 12 llegaremos a la conclusión de que la impedancia Z tiene un valor de

siendo φ

En el diagrama se ha supuesto que el circuito era inductivo ( ), pero en general se pueden dar los siguientes casos:
), pero en general se pueden dar los siguientes casos:
 : circuito inductivo, la intensidad queda retrasada respecto de la tensión (caso de la figura 12, donde φ es el ángulo de desfase).
: circuito inductivo, la intensidad queda retrasada respecto de la tensión (caso de la figura 12, donde φ es el ángulo de desfase). : circuito capacitivo, la intensidad queda adelantada respecto de la tensión.
: circuito capacitivo, la intensidad queda adelantada respecto de la tensión. : circuito resistivo, la intensidad queda en fase con la tensión (en este caso se dice que hay resonancia).
: circuito resistivo, la intensidad queda en fase con la tensión (en este caso se dice que hay resonancia).
Información extraida de: http://es.wikipedia.org/wiki/Circuito_el%C3%A9ctrico
















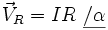





 representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina
representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina 








 es el módulo de la impedancia, ya que
es el módulo de la impedancia, ya que
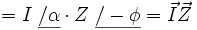 lo que significa que la impedancia es una magnitud compleja cuyo valor, según el triángulo de la figura 11, es:
lo que significa que la impedancia es una magnitud compleja cuyo valor, según el triángulo de la figura 11, es: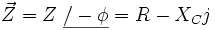


 ), pero en general se pueden dar los siguientes casos:
), pero en general se pueden dar los siguientes casos: : circuito capacitivo, la intensidad queda adelantada respecto de la tensión.
: circuito capacitivo, la intensidad queda adelantada respecto de la tensión. : circuito resistivo, la intensidad queda en fase con la tensión (en este caso se dice que hay
: circuito resistivo, la intensidad queda en fase con la tensión (en este caso se dice que hay